Grenzwerte von Funktionen für x → xₒ – h-Methode

in nur 12 Minuten? Du willst ganz einfach ein neues
Thema lernen in nur 12 Minuten?
-
 5 Minuten verstehen
5 Minuten verstehen
Unsere Videos erklären Ihrem Kind Themen anschaulich und verständlich.
92%der Schüler*innen hilft sofatutor beim selbstständigen Lernen. -
 5 Minuten üben
5 Minuten üben
Mit Übungen und Lernspielen festigt Ihr Kind das neue Wissen spielerisch.
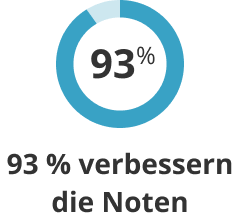
93%der Schüler*innen haben ihre Noten in mindestens einem Fach verbessert. -
 2 Minuten Fragen stellen
2 Minuten Fragen stellen
Hat Ihr Kind Fragen, kann es diese im Chat oder in der Fragenbox stellen.
94%der Schüler*innen hilft sofatutor beim Verstehen von Unterrichtsinhalten.
Grundlagen zum Thema Grenzwerte von Funktionen für x → xₒ – h-Methode
"h-Methode? Das kenne ich doch von der Ableitung." Genau. Bei den Ableitungen werden Grenzwertprozesse untersucht. Hier betrachten wir eine Funktion und ihr Verhalten bei einer Definitionslücke. Wir erstezen den Abstand zwischen x und x0 bei der Grenzwertbetrachtung für h und schreiben den Grenzwertprozess nach h um. Mit Hilfe dieser Methode kann man den Grenzwert ermitteln. Hierbei benötigst du die binomischen Formeln in der allgemeinen Form (a+b)n. Wenn du die binomischen Formeln aufgelöst hast, kürzt sich bestensfalls das h heraus und wir bekommen einen Grenzwert. Was sagt uns das jetzt? Ist x0 eine Polstelle oder eine hebbare Definitionslücke? Finde es heraus. Viel Spaß beim Lernen!
Grenzwerte von Funktionen für x → xₒ – h-Methode Übung
-
Beschreibe das Vorgehen bei der Bestimmung von Grenzwerten von Funktionen durch die h-Methode.
TippsWelche Bedeutung hat bei der Grenzweltbetrachtung $\lim\limits_{x \to x_0}$ das $x_0$?
Statt $x$ gegen $x_0$ gehen zu lassen, kann auch $x-x_0$ gegen 0 gehen.
LösungDie h-Methode ist eine Methode zur Bestimmung von Grenzwerten von Funktionen für $x\to x_0$ an einer Definitionslücke $x_0$. Dabei wird wie folgt vorgegangen:
- Bestimmung des Definitionsbereiches und der Definitionslücken
- Ersetzen von $x$: $x=h+x_0$
- Grenzweltbetrachtung von $\lim\limits_{h\to 0}$ statt $\lim\limits_{x \to x_0}$
- Anwenden von binomischen Formeln
- Kürzen von $h$ und Grenzwertberechnung
-
Bestimme den Grenzwert von $f(x)=\frac{x^3-2x+1}{x-1}$ an der Definitionslücke.
TippsDie Definitionslücke ist dadurch erklärt, dass an dieser Stelle die Funktion nicht definiert ist.
Statt $x$ gegen $x_0$ gehen zu lassen, kann auch $h:=x-x_0$ gegen 0 gehen.
Es gilt $(a+b)^3=a^3+3a^2b+3ab^2+b^3$.
LösungDie Definitionslücke der Funktion $f(x)=\frac{x^3-2x+1}{x-1}$ ist die Nennernullstelle, also $x_0=1$.
Anstatt nun $x$ gegen $x_0$ gehen zu lassen, kann auch $h=x-x_0$ gegen 0 gehen. Also ist $x=x_0+h$ und in diesem Beispiel $x=1+h$.
Der Grenzwert kann nun wie folgt berechnet werden:
- Anstatt den Grenzwert $\lim\limits_{x \to x_0} \frac{x^3-2x+1}{x-1}$ zu bestimmen, wird der Grenzwert $\lim\limits_{h\to 0} \frac{(h+1)^3-2(h+1)+1}{h}$ betrachtet.
- $(h+1)^3=h^3+3h^2+3h+1$. Also gilt mit Termumformungen, Kürzen von h und Anwendung der Grenzwertsätze für Summen:
-
Ermittle jeweils, wie x bei der Anwendung der h-Methode ersetzt wird.
TippsBestimme jeweils die Definitionslücke.
Bei der h-Methode wird der Grenzwert $x$ gegen $x_0$ ersetzt durch $h=x-x_0$ gegen 0.
LösungDie h-Methode ist ein Verfahren zur Bestimmung von Grenzwerten von Funktionen für $x \to x_0$ an einer Definitionslücke $x_0$. Hierbei wird wie folgt ersetzt: $x=x_0+h$. Somit kann der Grenzwert für $h\to 0$ betrachtet werden.
- $\mathbf{\frac{x^4-x-2}{x+1}}$: Hier ist $x_0=-1$ und somit $x=-1+h=h-1$.
- $\mathbf{\frac{x^3+1}{x-1}}$: Hier ist $x_0=1$ und somit $x=1+h=h+1$.
- $\mathbf{\frac{x^4-16}{x+2}}$: Hier ist $x_0=-2$ und somit $x=-2+h=h-2$.
- $\mathbf{\frac{x^2+2x-3}{x+3}}$: Hier ist $x_0=-3$ und somit $x=-3+h=h-3$.
-
Untersuche die Funktion $f(x)=\frac{x^3-8}{x-2}$ auf Konvergenz an der Definitionslücke.
TippsEs gilt $(a+b)^3=a^3+3a^2b+3ab^2+b^3$.
Wenn der Grenzwert existiert, so lässt sich $h$ kürzen.
LösungDie Definitionslücke von $f(x)=\frac{x^3-8}{x-2}$ ist $x_0=2$. Statt den Grenzwert von $x$ gegen 2 zu betrachten, kann auch der von $h=x-2$ gegen 0 betrachtet werden. Dies führt zu der Ersetzung von $x$ durch $x=2+h$.
$\begin{align*} \lim\limits_{h\to 0} \frac{(2+h)^3-8}{h}&= \lim\limits_{h\to 0} \frac{8+12h+6h^2+h^3-8}{h}\\ &=\lim\limits_{h\to 0} \frac{h^3+6h^2+12h}{h} \end{align*}$
Hier wurde die Formel $(a+b)^3=a^3+3a^2b+3ab^2+b^3$ mit $a=2$ und $b=h$ verwendet.
$\lim\limits_{h\to 0} \frac{h^3+6h^2+12h}{h} =\lim\limits_{h\to 0} \frac{h(h^2+6h+12)}{h}$
Nun kann $h$ gekürzt und der Grenzwert berechnet werden.
$\lim\limits_{h\to 0} \frac{h(h^2+6h+12)}{h}=\lim\limits_{h\to 0} (h^2+6h+12)=12$.
-
Benenne die drei Verfahren zur Bestimmung von Grenzwerten von Funktionen für $x\to x_0$ mit Definitionslücke $x_0$.
TippsEs gibt Grenzwertsätze zur Berechnung von Grenzwerten, welche Aussagen darüber treffen, wie Grenzwerte von Summenfunktionen, Differenzfunktionen, Produktfunktionen und Quotientenfunktionen berechnet werden können.
Der $\epsilon$-Schlauch wird zur Erklärung eines Grenzwertes betrachtet.
LösungDer Grenzwert einer Funktion an einer Definitionslücke kann berechnet werden, indem
- man verschiedene $x$-Werte, welche sich dem $x_0$ nähern, in die Funktionsgleichung einsetzt. Das wird als Testeinsetzung bezeichnet.
- man den Term, dessen Grenzwert berechnet werden soll, umformt. Dies geschieht zum Beispiel durch binomische Formeln oder durch Polynomdivision. Dabei handelt es sich um eine Termumformung.
- man die Grenzwertbetrachtung $\lim\limits_{x \to x_0}$ ersetzt durch $\lim\limits_{h \to 0}$, wobei $h=x-x_0$ ist. Das ist unter dem Stichwort h-Methode bekannt.
-
Ermittle den Grenzwert der Funktion $f(x)=\frac{x^4-16}{x-2}$ an der Definitionslücke.
TippsBestimme zunächst die Stelle $x_0$, wo die Funktion nicht definiert ist, und ersetze $x=x_0+h$.
Es gilt $(a+b)^4=a^4+4a^3b+6a^2b^2+4ab^3+b^4$.
Es gilt $(2+h)^4=16+32h+24h^2+8h^3+h^4$.
LösungZunächst wird die Definitionslücke bestimmt. Diese ist die Nennernullstelle, also $x_0=2$.
Nun wird wie folgt ersetzt: $x=2+h$.
In der Grenzwertberechnung $\lim\limits_{x \to 2} \frac{x^4-16}{x-2}$ wird $x \to 2$ durch $h \to 0$ ersetzt und $x$ wie oben angegeben:
$\lim\limits_{h\to 0}\frac{(2+h)^4-16}{h}=\lim\limits_{h\to 0}\frac{16+32h+24h^2+8h^3+h^4-16}{h}$.
Dies erhält man unter Verwendung der Formel $(2+h)^4=16+32h+24h^2+8h^3+h^4$. Der Term ohne $h$ fällt heraus und $h$ kann ausgeklammert werden:
$\begin{align*} \lim\limits_{h\to 0}\frac{16+32h+24h^2+8h^3+h^4-16}{h}&=\lim\limits_{h\to 0}\frac{32h+24h^2+8h^3+h^4}{h}\\ &=\lim\limits_{h\to 0}\frac{h(32+24h+8h^2+h^3)}{h} \end{align*}$
Nun wird $h$ gekürzt und somit der Grenzwert berechnet:
$\lim\limits_{h\to 0}\frac{h(32+24h+8h^2+h^3)}{h}=\lim\limits_{h\to 0}(32+24h+8h^2+h^3)=32$.
9.295
sofaheld-Level
6.600
vorgefertigte
Vokabeln
8.194
Lernvideos
38.687
Übungen
33.496
Arbeitsblätter
24h
Hilfe von Lehrkräften

Inhalte für alle Fächer und Klassenstufen.
Von Expert*innen erstellt und angepasst an die Lehrpläne der Bundesländer.
Testphase jederzeit online beenden
Beliebteste Themen in Mathematik
- Römische Zahlen
- Prozentrechnung
- Prozentrechnung - Übungen
- Primzahlen
- Geometrische Lagebezeichnungen
- Was ist eine Ecke?
- Rechteck
- Was ist eine Gleichung?
- Pq-Formel
- Binomische Formeln
- Trapez
- Volumen Zylinder
- Potenzgesetze – Übungen
- Umfang Kreis
- Zehnerzahlen vergleichen und ordnen – Übungen
- Quadrat
- Zahlen sortieren – Übungen
- Division
- Binomische Formeln – Übungen
- Raute
- Parallelogramm
- Ungleichungen – Übungen
- Polynomdivision
- Zahlen bis 1000 ordnen – Übungen
- Was Ist Eine Viertelstunde
- Terme mit Variablen aufstellen – Übungen
- Prisma
- Die Grundrechenarten – Übungen
- Mitternachtsformel
- Äquivalenzumformung
- Grundrechenarten Begriffe
- Größer Kleiner Zeichen
- Dreiecksarten
- Punkt-vor-Strich und Klammern-zuerst-Regel
- Aufbau von Dreiecken
- Quader
- Zahlen runden – Übungen
- Satz Des Pythagoras
- Ziffern und Stellenwerte – Übungen
- Dreieck Grundschule
- Koordinatensystem – Übungen
- Erste Binomische Formel
- Kreis
- Trigonometrie
- Trigonometrische Funktionen
- Standardabweichung
- Quadratische Gleichungen – Übungen
- Flächeninhalt
- Termumformungen – Übungen
- Volumen Kugel

 5 Minuten verstehen
5 Minuten verstehen
 5 Minuten üben
5 Minuten üben
 2 Minuten Fragen stellen
2 Minuten Fragen stellen




